T1 一路向北 south:
首先将题意转化,我们要求出的是两两山峰之间的 “最大瓶颈路”(即路径上最小边最大的路径)。
首先将图缩成若干连通块,之间相邻的连边后,建出“最大生成树”,那么两个点之间的最大瓶颈路就是树上路径。
设连通块个数为 $k$,$k$ 最大为 $n\times m$,我们通过暴力统计两两山峰的最大瓶颈路有了一个 $\mathcal{O(k\log{k} + k^2)}$ 的做法。
考虑如何优化,我们发现在通过 kruskal 生成最大生成树的时候,每条边加进去连接两个连通块,若某个连通块内有没有更新答案的峰,且另外一个连通块的最高峰比它高的时候,就可以更新它的答案。
我们用 vector 存储一个连通块内没有更新答案的点集,然后启发式合并即可,复杂度 $\mathcal{O(k\log{k})}$。
code:
int n, m, cnt, mnt;
int f[2005][2005], t[2005][2005], p[L], ans[L];
bool mou[L];
int dx[] = {0, 0, 1, -1, 1, -1, 1, -1};
int dy[] = {1, -1, 0, 0, 1, -1, -1, 1};
vector<pii> e[L];
vector<pair<int, pii> > edges;
vector<pii> Tans;
bool check(int x, int y) {
if(x > n || y > m || x < 1 || y < 1) return false;
return true;
}
void dfs(int x, int y, int id) {
t[x][y] = id;
rep(i, 0, 7) if(check(x + dx[i], y + dy[i]) && f[x][y] == f[x + dx[i]][y + dy[i]] && !t[x + dx[i]][y + dy[i]]) {
dfs(x + dx[i], y + dy[i], id);
}
}
namespace Merge {
vector<int> nds[L];
int fa[L], siz[L];
void init() {
rep(i, 1, cnt) {
fa[i] = i; if(mou[i]) nds[i].pb(i); siz[i] = 1;
}
}
int getfa(int x) {
return (x == fa[x]) ? x : (fa[x] = getfa(fa[x]));
}
void merge(int a, int b, int c) {
a = getfa(a), b = getfa(b);
if(siz[a] > siz[b]) swap(a, b);
if(a == b) return ;
fa[a] = b; siz[b] += siz[a];
while(!nds[a].empty() && !nds[b].empty() && p[nds[a][nds[a].size() - 1]] < p[nds[b][0]]) ans[nds[a][nds[a].size() - 1]] = c, nds[a].pop_back();
while(!nds[a].empty() && !nds[b].empty() && p[nds[b][nds[b].size() - 1]] < p[nds[a][0]]) ans[nds[b][nds[b].size() - 1]] = c, nds[b].pop_back();
rep(i, 0, signed(nds[a].size() - 1)) nds[b].pb(nds[a][i]);
}
}
signed main() {
rd(n, m);
rep(i, 1, n) rep(j, 1, m) rd(f[i][j]);
rep(i, 1, n) rep(j, 1, m) if(!t[i][j]) { dfs(i, j, ++ cnt); p[cnt] = f[i][j]; }
rep(i, 1, n) rep(j, 1, m) {
rep(k, 0, 7) {
int x = i + dx[k], y = j + dy[k]; if(!check(x, y)) continue;
if(t[x][y] != t[i][j]) e[t[i][j]].pb({t[x][y], min(f[x][y], f[i][j])});
}
}
rep(i, 1, cnt) {
sort(e[i].begin(), e[i].end());
e[i].erase(unique(e[i].begin(), e[i].end()), e[i].end());
for(auto v : e[i]) {
edges.pb({v.second, {i, v.first}});
}
}
rep(i, 1, cnt) {
mou[i] = true;
for(auto v : e[i]) if(p[v.first] > p[i]) mou[i] = false;
if(mou[i]) mnt ++;
}
Merge::init();
sort(edges.begin(), edges.end(), [](pair<int, pii> a, pair<int, pii> b) { return a.first > b.first; });
rep(i, 0, signed(edges.size() - 1)) {
Merge::merge(edges[i].second.first, edges[i].second.second, edges[i].first);
}
rep(i, 1, cnt) {
if(mou[i]) {
Tans.pb({p[i], ans[i]});
}
}
int T = 0;
rep(i, 1, cnt) {
T += Merge::siz[i];
}
sort(Tans.begin(), Tans.end(), [](pii a, pii b) { return a > b; } );
cout << mnt << endl;
for(auto v : Tans) {
cout << v.first << ' ' << v.second << '\n';
}
return 0;
}T2 飘移 drift
构造题。
考虑每个点度数较小的情况,不难发现我们可以把边看作边,然后暴力将连接一个点之间的边暴力两两连边,然后跑最短路。
原图:
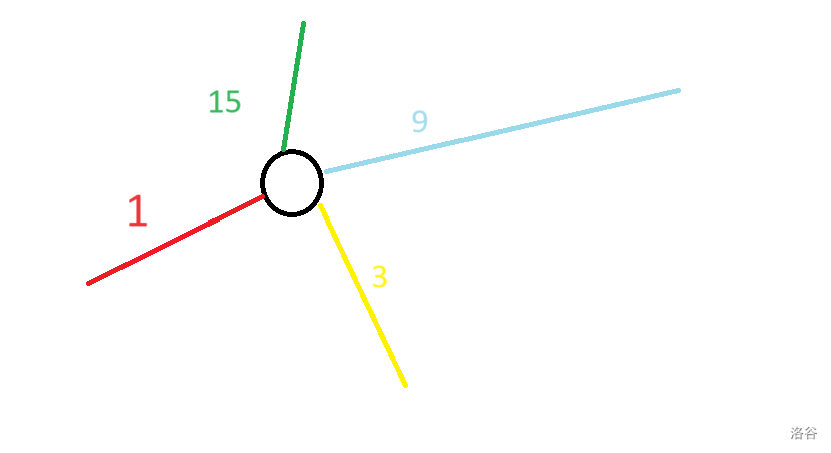
建图(暴力,我们将边看作点):
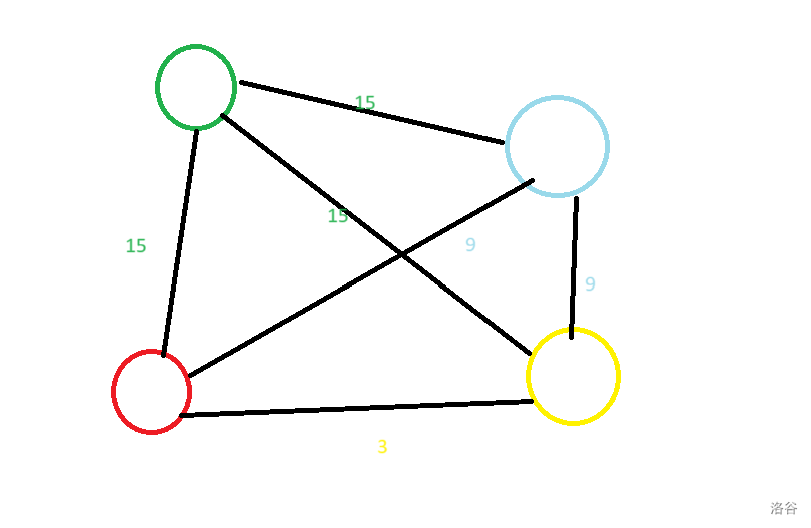
但是我们发现这种方法边数可以被卡到 $m^2$ 级别(菊花图)。
考虑如何优化这个过程。
我们发现,一个边往比自己大的边走是需要补代价的,往比自己小的点走不用补代价。
短暂思索后,发现可以将原图上的边按照边权排序,设 A < B < C(边权)。
A 到 C 的代价即为 A 到 B 的代价再加上 B 到 C 的代价。
然后可以构建出下面这张图。
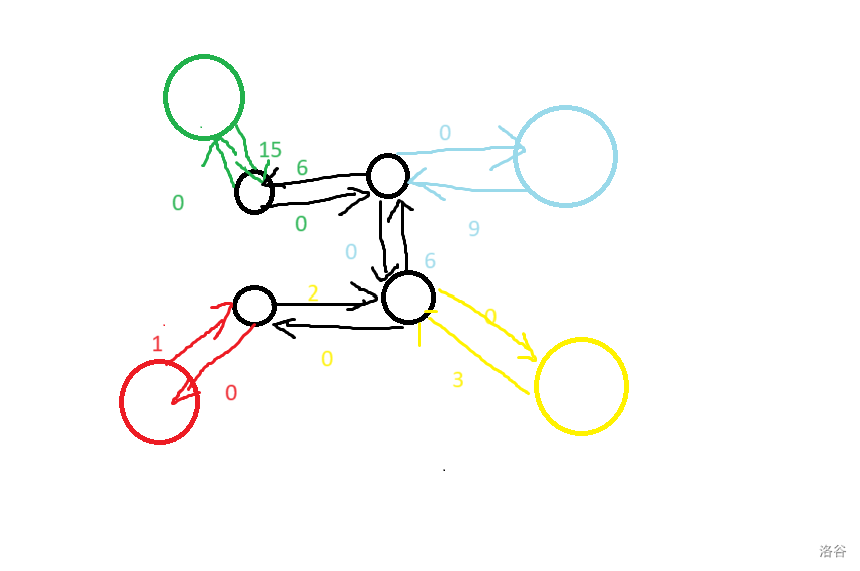
我们对于每个边点的一端都建出一个辅助点,辅助点向第一个比自己大的点连有向边,边权为需补的代价,向比自己第一个小的点连有向边,边权为 0,因为不用补代价。
至此,本题解决,我们需要建 $3 \times m$ 左右个点,以及 $6 \times m$ 条边,然后在上面跑最短路即可。复杂度 $\mathcal O(m\log m)$。
code:
int n, m, cnt, dis[L];
struct node {
int u, v, w;
} f[L];
vector<pii> nds[L];
vector<pii> e[L];
void dij(int u) {
dis[u] = inf; priority_queue<pii, vector<pii>, greater<pii> > p; p.push({0, u});
while(!p.empty()) { auto tp = p.top(); p.pop(); int u = tp.second;
if(dis[u] != inf) continue;
dis[u] = tp.first;
for(auto v : e[u]) {
if(dis[v.first] == inf) p.push({v.second + dis[u], v.first});
}
}
}
signed main() {
rd(n, m);
f[1].u = 0, f[1].v = 1, f[1].w = 0;
rep(i, 2, m + 1) rd(f[i].u, f[i].v, f[i].w);
f[m + 2].u = n + 1, f[m + 2].v = n, f[m + 2].w = 0;
cnt = m + 2;
rep(i, 1, m + 2) {
e[i].pb({++ cnt, f[i].w});
e[cnt].pb({i, 0});
nds[f[i].v].pb({i, cnt});
e[i].pb({++ cnt, f[i].w});
e[cnt].pb({i, 0});
nds[f[i].u].pb({i, cnt});
}
rep(i, 1, n) sort(nds[i].begin(), nds[i].end(), [&](pii a, pii b) { return f[a.first].w < f[b.first].w; }); //
rep(i, 1, n) {
rep(j, 0, signed(nds[i].size()) - 2) {
e[nds[i][j].second].pb({nds[i][j + 1].second, f[nds[i][j + 1].first].w - f[nds[i][j].first].w});
e[nds[i][j + 1].second].pb({nds[i][j].second, 0});
}
}
rep(i, 1, cnt) dis[i] = inf; dij(1);
cout << dis[m + 2] << endl;
return 0;
}T3 暗号 signal
一道非常小清新的思维题。
不难发现,我们每次可以选择交换 $xi$ 和 $x{i \times 2}$,以及 $xi$ 和 $x{i \times 2 + 1}$ ,请记住,这两个交换是有序的,即我们只能选择前操作后再选择后操作。
那么这个问题就转化到一个二叉树上,我们每次可以选择按照 bfs 序选择是否与左儿子交换,是否与右儿子交换。
我们接下来分析这个过程,我们设父亲,左儿子,右儿子分别为 $a, b, c$。
若 $a = \min(a, b, c)$,我们显然不会和左儿子和右儿子交换,所以显然是不变的。
若 $b = \min(a, b, c)$,我们显然会和左儿子交换,然后不会和右儿子交换。
若 $c = \min(a, b, c)$,我们显然会和右儿子交换,但是是否第一次与左儿子交换,我们并不知道。
我们设 $w = \min(a, b)$,我们假设将 $w$ 放入左子树,它最终会落到 $p1$ 位置,放入右子树,它最终会落到 $p2$ 位置,若 $p1 < p2$,我们会将 $w$ 放入左子树,否则放入右子树。
考虑正确性,若我们将较大数放入那一边,则 $\min(p1, p2)$ 的字符显然会变大,且我们从当前子树位置到 $\min(p1, p2) - 1$ 的字符是不受影响的。
我们设 $f_{i,j}$ 表示,将 $j$ 放置在 $i$ 位置最后会落到哪里。不难发现,我们对于每个 $i$ 查询的一定是它的祖先的节点,或者它祖先的左或右儿子,我们可以预处理出来,由于在一颗特殊二叉树上,层高是 $\log n$ 级别的,预处理复杂度 $\mathcal O(n\log n)$,贪心复杂度 $\mathcal O(n)$。
当然,我们也可以不预处理,使用 map 进行记忆化,复杂度 $\mathcal O(n\log^2 n)$。
code:
#define mi(a, b, c) min(a, min(b, c))
int n, a[L];
vector<int> nums;
bool ban[L];
map<pii, int> tmp;
int check(int x, int f) {
if(tmp[{x, f}]) return tmp[{x, f}];
int l = (x << 1), r = (x << 1 | 1);
if(l <= n && r <= n) {
if(f == mi(a[l], a[r], f)) return tmp[{x, f}] = x;
else if(a[l] == mi(a[l], a[r], f)) return tmp[{x, f}] = check(l, f);
else {
int _x = a[l], _y = f; if(_x > _y) swap(_x, _y);
int p1 = check(l, _x), p2 = check(r, _x);
if(p1 < p2)
return tmp[{x, f}] = ((_x == f) ? p1 : check(r, f));
else
return tmp[{x, f}] = ((_x == f) ? p2 : check(l, f));
}
} else if(l <= n) {
if(f == min(a[l], f)) return tmp[{x, f}] = x;
else return tmp[{x, f}] = check(l, f);
} else {
return tmp[{x, f}] = x;
}
}
signed main() {
rd(n); rep(i, 1, n) rd(a[i]);
rep(i, 1, n) {
int l = (i << 1), r = (i << 1 | 1);
if(l <= n && r <= n) {
if(a[i] == mi(a[i], a[l], a[r])) continue;
else if(a[l] == mi(a[i], a[l], a[r])) swap(a[l], a[i]);
else {
int x = a[l], y = a[i]; if(x > y) swap(x, y);
int p1 = check(l, x), p2 = check(r, x);
if(p1 < p2) a[i] = a[r], a[l] = x, a[r] = y;
else a[i] = a[r], a[r] = x, a[l] = y;
}
} else if(l <= n) {
if(a[i] == min(a[i], a[l])) continue;
else if(a[l] == min(a[i], a[l])) swap(a[l], a[i]);
}
}
rep(i, 1, n) printf("%d%c", a[i], i == n ? '\n' : ' ');
return 0;
}T4 不该 none
原来题解写的过于抽象了,现在重构一下,其实重构后也很抽象,大家可以看一下这位大佬写的 题解。如果你想看我原来的抽象题解的话,也可以点这里。
首先我们发现,我们可以将第 $i$ 个人需要在 $[l_i, r_i]$ 的小组中转化成,小组要取出恰好 $k$ 个人,满足 $l_j \leq k \leq r_j$,我们可以将 $(l_i, r_i)$ 放置于二维平面上,每次要从一个长方形内取出 $k$ 个点。
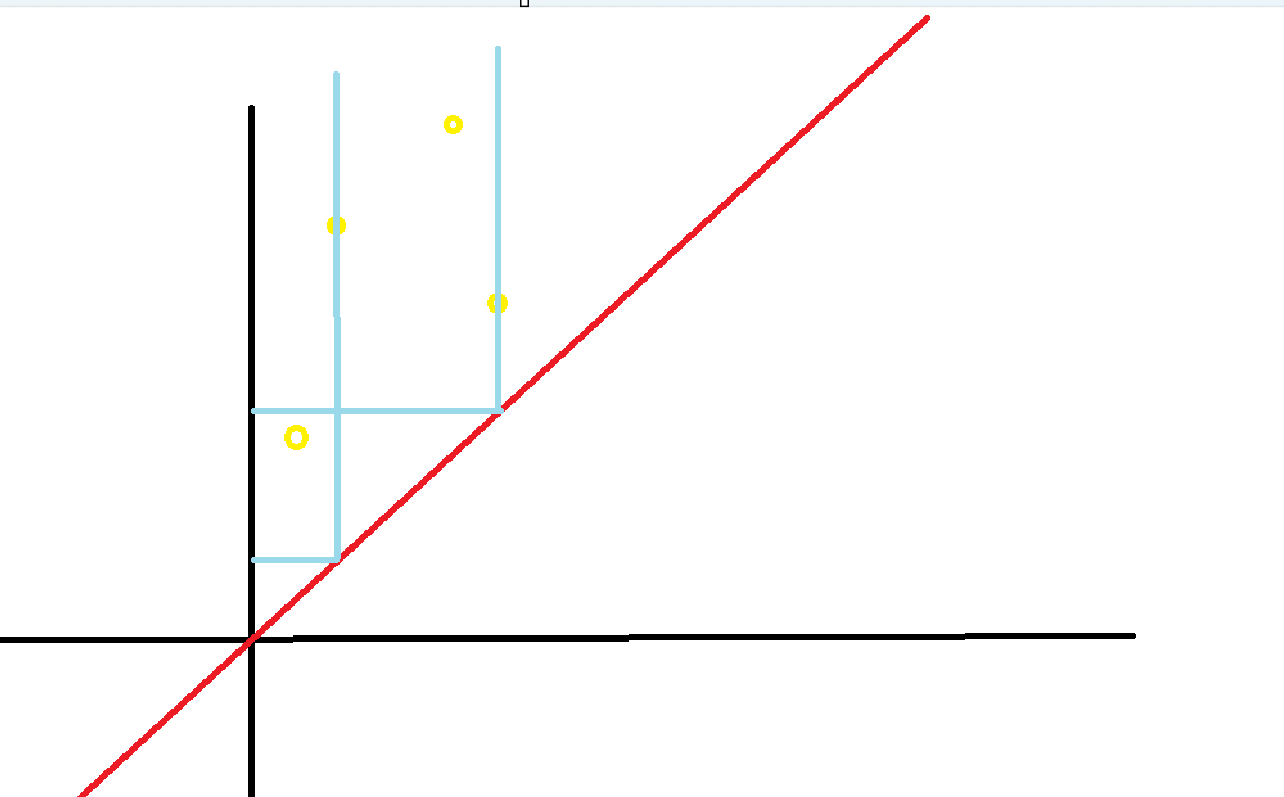
对于静态的二维数点问题,我们可以使用主席树完成。
显然,若 $m = 1$,我们可以直接做,由于每天询问之间独立,我们每天二维数点即可。
考虑 $m > 1$,我们将询问 $k_i$ 从小到达排序。
我们发现询问之间可能冲突,即,我在 $k_1$ 时选的点可能在 $k_2$ 查询时也能用上。
那么,我们肯定是每次贪心选择 $y$ 坐标较低的点。
我们假设对于每次询问后,保留如下内容:
$high, q$,分别表示我们此时对于 $x \leq k$ 剩下能选的的最低点,以及我们剩下能选的点的个数。
如果我们存在一段使得 $high_{i - 1} > highi$,我们就将 $high{i - 1}$ 设置为失效状态,这是显然的,因为我这次选择必然将 $high_{i - 1}$ 那个高度点用掉了。那么有效状态的 $high$ 显然是单调的。(如果这段看不大懂可以先看下面几个段,然后回来看)
我们不难发现 $high$ 一定是单调递减的,用单调栈维护。
我们发现如果我们此次查询的 $k > high_{last}$,那么上一次维护的 $q$ 就没必要存在了,设置为失效,我们一直倒退到 $k \leq high$,然后来查询剩下合法数量 $tot$,若 $tot < k$,显然无解,否则,我们尝试找到若干高度尽量低的点。
我们如何找到高度尽量低的点呢?我们发现栈是单调递减的,若我们用栈最后一部分的那个区间能获取出 $k$ 个点,且剩余点的最低位置 $H > high{lst}$,那么显然,我们就用这些了,否则我们可以继续均摊,使得最低高度不用那么高,即我们将最后一段 $< high{lst}$ 且合法的点拿出来,然后合并两段。
code:
int n, T;
int a[L], b[L];
vector<int> e[L];
int k[L];
namespace segment_tree {
#define mid (l + r >> 1)
#define lson L, R, l, mid, tree[w].l
#define rson L, R, mid + 1, r, tree[w].r
int cnt = 0;
const int L = 4e7 + 5;
int root[L];
struct node {
int l, r, num;
} tree[L];
int clone(int w) {
int nw = ++ cnt;
tree[nw] = tree[w];
return nw;
}
void pushup(int w) {
tree[w].num = tree[tree[w].l].num + tree[tree[w].r].num;
}
int modify(int L, int R, int l, int r, int w, int num) {
w = clone(w);
if(L <= l && r <= R) { tree[w].num ++; return w; }
if(R <= mid) tree[w].l = modify(lson, num);
else if(mid < L) tree[w].r = modify(rson, num);
else tree[w].l = modify(lson, num), tree[w].r = modify(rson, num);
pushup(w);
return w;
}
int query(int L, int R, int l, int r, int w) {
if(L <= l && r <= R) return tree[w].num;
if(R <= mid) return query(lson);
else if(mid < L) return query(rson);
else return query(lson) + query(rson);
}
int build(int l, int r, int w) {
if(l != r)
tree[w].l = build(l, mid, ++ cnt), tree[w].r = build(mid + 1, r, ++ cnt), pushup(w);
else
tree[w].num = 0;
return w;
}
}
using segment_tree::build;
using segment_tree::root;
using segment_tree::modify;
using segment_tree::query;
using segment_tree::tree;
int QueryH(int L, int R, int l, int r, int num) {
if(l == r) return l;
if(num > tree[tree[R].r].num - tree[tree[L].r].num) return QueryH(tree[L].l, tree[R].l, l, (l + r >> 1), num - (tree[tree[R].r].num - tree[tree[L].r].num));
else return QueryH(tree[L].r, tree[R].r, (l + r >> 1) + 1, r, num);
}
int s[L], q[L], high[L];
signed main() {
n = read();
rep(i, 1, n) {
a[i] = read(), b[i] = read();
e[a[i]].push_back(b[i]);
}
root[0] = build(1, n, 0);
rep(i, 1, n) {
root[i] = root[i - 1];
for(auto d : e[i]) root[i] = modify(d, d, 1, n, root[i], 1);
}
T = read();
while(T --) {
int m = read();
rep(i, 1, m) k[i] = read();
sort(k + 1, k + 1 + m);
int Top = 0;
rep(i, 1, m) {
while(high[Top] < k[i] && Top) Top --;
int tot = query(k[i], n, 1, n, root[k[i]]) - query(k[i], n, 1, n, root[s[Top]]) + q[Top] - k[i];
if(tot < 0) {
puts("0");
goto leave;
}
int H = QueryH(root[s[Top]], root[k[i]], 1, n, tot - q[Top]);
while(high[Top] < H && Top) Top --, H = QueryH(root[s[Top]], root[k[i]], 1, n, tot - q[Top]);
Top ++;
s[Top] = k[i], q[Top] = tot, high[Top] = H;
}
puts("1");
leave:;
}
return 0;
}